Analysis of Math Pass Rates by Instructor
Prepared by Jeff Webb
AAB 355-Q • 4600 S Redwood Road • (801) 957-4110
March 3, 2016
Abstract
In earlier research we showed that variation in pass rates between math sections was consistent with a random process (“Draft: Variation in Math Student Pass Rate by Section and Instructor,” October 2, 2015). That is, the variation observed in pass rates in individual classes can be generated randomly from the binomial distribution with probability equal to the overall pass rate (in this case we used .6). This doesn't necessarily prove that pass rates at the section level are random but does support what we might call the luck of the draw argument: the idea that wide variation in math pass rates is due to factors outside of the instructor’s control, such as (perhaps primarily) student ability and preparation. However, we also showed that the variation in pass rates across instructors was not consistent with a random process. In particular, some instructors had pass rates that were lower than could be generated randomly, while some had pass rates that were higher, suggesting that something more than luck of the draw was at work in instructor-level pass rates. What is that something? Are instructors with low pass rates simply less effective at teaching the material, or do they have harder grading standards, or is there some other systematic reason for student under-performance in their classes—perhaps the courses they routinely teach are harder, the student populations they serve less able, or their most frequent delivery methods (such as online) less successful? It is difficult to distinguish between these possibilities. In what follows we seek to shed some light on the issue of instructor pass rates by controlling statistically for possibly confounding factors, and considering how students perform in subsequent math courses with different instructors.
Key Findings
- Instructor pass rates differed significantly from each other and from the average, particularly at the low and high ends of the distribution, even after accounting for confounding factors such as prior grade, instructor status, course level and delivery type.
- Students of low pass rate instructors received higher grades in their next math course and students of high pass rate instructors received lower grades. (This was true for students repeating courses as well.) There was, in other words, are rebound effect in the first case and a regression effect in the second. These patterns tend to support the idea that differences in instructor pass rates, while not entirely extricable from other factors such as teaching quality, are due to differences in grading standards.
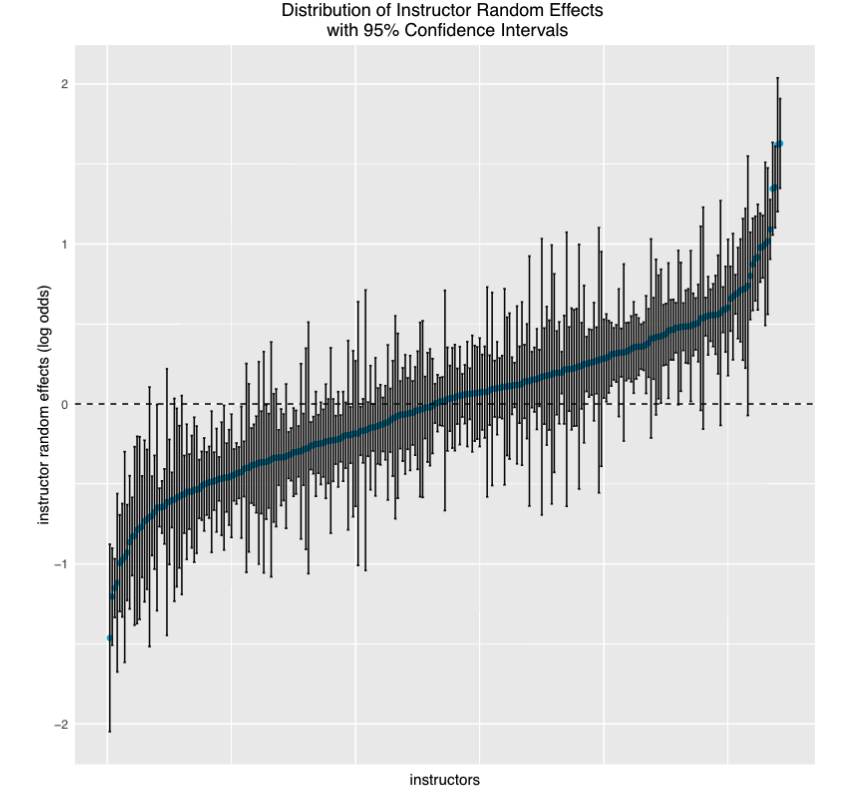
Figure 1. Individual instructors are on the x-axis, sorted low to high by random effects coefficients on the y-axis. These are estimated differences in pass rates, expressed in log odds. (The scale of the y-axis is unimportant in this context, as we are only looking to see whether the pass rates associated with instructors were significantly different.) The vertical bars represent the 95% confidence intervals for the point estimates. Non-overlapping bars represent significant differences between instructors. We can see that, especially at the tails of the distribution, instructors were often not only different from each other but also from the average instructor (represented here by the dashed center line). These results suggest that there are indeed significant differences among instructors that cannot be explained by luck of the draw—by student preparation (or, indeed, by any differences associated with students), by delivery type, by instructor status, or by courses taught. One of the handy things about mixed effects models is that they allow us to quantify how much of the variation in the data is attributable to the random effects variables—in this case to differences between students, between courses, and between instructors. After accounting for the fixed effects, differences between students accounted for 13% of the remaining variance, while instructors and courses accounted for 10% and 7% respectively.
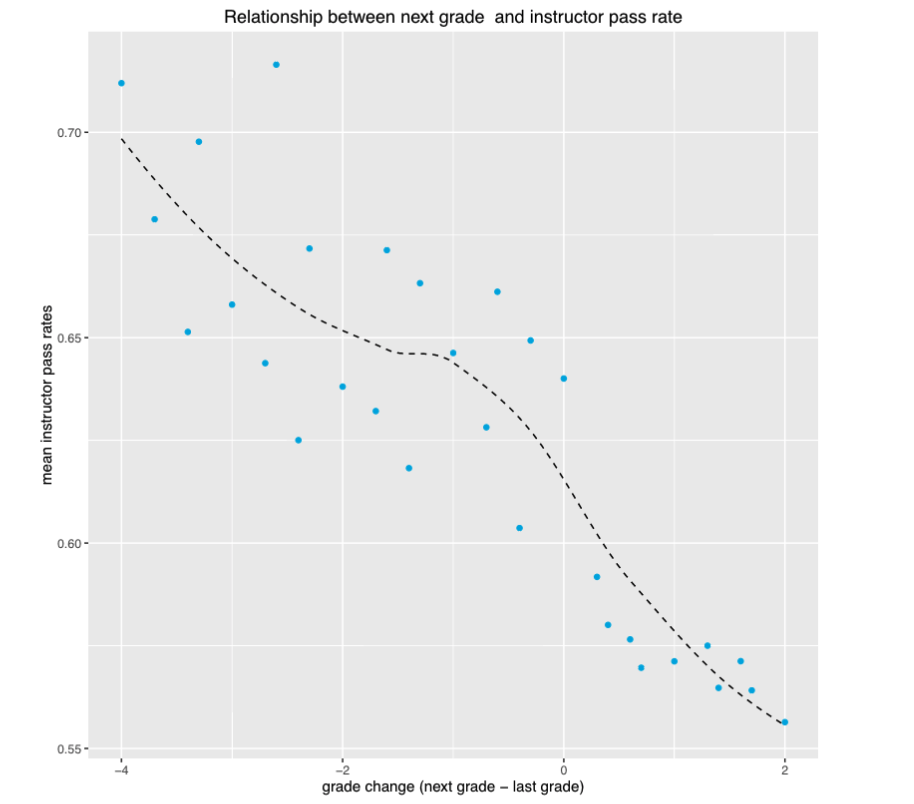
Figure 2. The x-axis in the above plot represents a student’s grade change in the next math course after the reference course. The max is 2 because this plot included only students who passed the reference course with a C or better. Thus the maximum possible increase (from C to A, or, numerically, from 2 to 4) was 2, while the minimum was -4 because students who received an A in the reference course could have dropped to an E in the next course (4 to 0). The y-axis represents the mean of the instructor pass rates at that grade difference increment. So while there were many instructors of students who dropped 4 grade points in their next class (represented by -4 on the x-axis), this plot summarizes these multiple instructor pass rates by taking the mean of their pass rates. There was a strong negative relationship between grade difference and instructor pass rates such that students taught by instructors with high pass rates tended to have lower grades in their next math courses (which we might call a regression effect), while those taught by instructors with low pass rates tended to have higher grades (rebound effect). Thus, in general, we see a grade rebound for students whose last grade was from a instructor with a low pass rate and a grade regression for students whose last grade was from a instructor with a high pass rate. Both these effects—the rebound and the regression— would be consistent with the idea that differences in instructor pass rates derive from differences not in instructional quality but in grading standards. Why? If the difference were due to instructional quality we might expect to see increased ability reflected in the next grade: students would learn more and with improved mathematical abilities earn a higher grade in the next class.
(requires College login)